35.4. Поперечный изгиб

35.4.3. Напряжения при изгибе

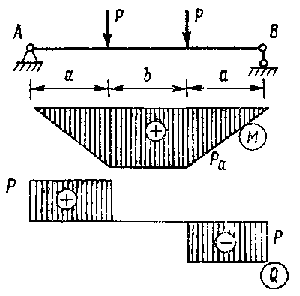
        Ранее было установлено, что при нагрузке, перпендикулярной оси балки, в каждом ее сечении могут возникать одновременно изгибающий момент и поперечная сила. При изучении напряженного состояния балки удобнее начинать с частного случая, когда поперечная сила равна нулю, т. е. с чистого изгиба. Так, в средней части балки (рис. 9.30), собственным весом которой пренебрегаем, между точками приложения сил Р возникает только изгибающий момент, а поперечная сила отсутствует, т. е. имеет место чистый изгиб. Будем считать, что поперечное сечение нашей балки обладает хотя бы одной осью симметрии, которая совпадает с силовой плоскостью. Таким образом, одна из главных осей инерции сечения лежит в плоскости изгиба, а другая перпендикулярна ей.

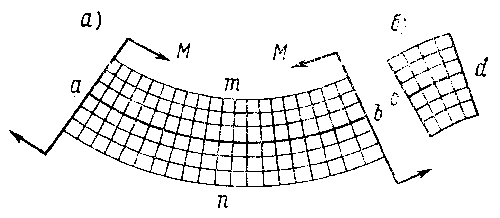
        Характер деформации при чистом изгибе удобнее всего проследить на резиновом брусе прямоугольного сечения с нанесенной на его поверхность сеткой (рис. 9.31).

        Так как продольные волокна балки деформируются тем больше, чем дальше они отстоят от нейтральной оси, деформации, а значит и напряжения в поперечном сечении прямо пропорциональны (рис. 9.32) расстоянию от нейтральной оси до рассматриваемой точки сечения.
        Нейтральная ось проходит через центр тяжести сечения, и напряжения на нейтральной оси равны нулю. Расчетной характеристикой для подбора балок является максимальное значение . Эпюра на рис. 9.32 показывает, что возникают в верхнем и нижних волокнах, отстоящих от нейтральной оси на . Напряжение в волокнах, отстоящих от нейтральной оси на величину у, равно:

	Рис. 9.32. Нормальные напряжения при чистом изгибе.

        Для того чтобы соблюдалось условие равновесия, момент, образованный напряжениями, должен быть равен изгибающему моменту в этом сечении. Из этого условия можно определить . Подсчитаем, какой момент создают напряжения относительно нейтральной оси.
        Выделим в сечении участок площадью и, считая напряжения в пределах этого участка постоянными, соберем их. Получим силу , которую можно подсчитать по формуле


Момент силы равен:


Полный момент напряжений


где - момент инерции сечения относительно нейтральной оси.


Следовательно, полный момент можно записать:


где М - изгибающий момент в данном сечении. Отсюда

(9.28)

Величина - это момент сопротивления при изгибе . Таким образом,

(9.29)

        Если нас интересует не в сечении, а напряжение в любой точке, лежащей на горизонтальной линии поперечного сечения бруса на расстоянии у от нейтральной оси, то для его вычисления формулу (9.28) надо представить в виде

(9.30)

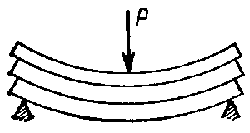
        В отличие от чистого изгиба при поперечном изгибе в сечениях бруса возникает не только изгибающий момент, но и поперечная сила. Поэтому в поперечном сечении наряду с нормальными напряжениями появляются также и касательные напряжения .
        Касательные напряжения обладают свойством взаимности, т. е. они возникают всегда по взаимно перпендикулярным площадкам. Из этого следует, что если касательные напряжения при изгибе балок возникают в сечениях, перпендикулярных оси балки, то в сечениях, параллельных нейтральному слою, они тоже возникают. Касательные напряжения, действующие по плоскостям, параллельным нейтральному слою, стремятся сдвинуть горизонтальные слои в балке по отношению друг к другу.
        Если балку составить из горизонтальных пластинок, свободно лежащих друг на друге, то при изгибе эти пластинки сдвинутся и край балки примет ступенчатое очертание (рис. 9.33). Если теперь склеить пластинки, то сдвига не произойдет, зато возникнут касательные напряжения, препятствующие сдвигу.

	Рис. 9.33. Возникновение касательных напряжений при изгибе.

        Впервые установил наличие касательных напряжений при изгибе Д. И. Журавский. Он же предложил и формулу для их расчета (9.31), которая теперь носит его имя:

(9.31)

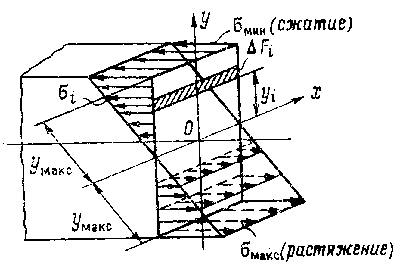
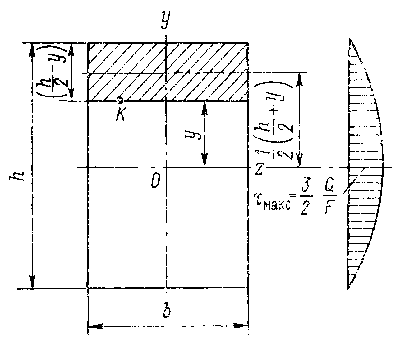
        Итак, касательное напряжение в предельном слое балки на расстоянии у от нейтральной оси (рис. 9.34) равно произведению поперечной силы Q на статический момент 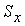части поперечного сечения, лежащий выше (или ниже) рассматриваемого слоя относительно нейтральной оси (на рис. 9.34 заштрихована), деленному на момент инерции всего сечения относительно нейтральной оси и на ширину b поперечного сечения в том месте, где определяется касательное напряжение.

	Рис. 9.34. Схема к расчету касательных напряжений в поперечном сечении балки.

        Расчеты, проведенные по этой формуле для поперечных сечений различной формы, показали, что максимальные касательные напряжения возникают в нейтральном слое, т. е. в плоскости, проходящей через центр тяжести сечения (см. рис. 9.34).
        Для прямоугольного сечения:

(9.32)

        для круглого сечения

(9.33)

       
        для двутаврового сечения

(9.33 a)

        В формулах (9.32) и (9.33) F - это площадь сечения. В формуле (9.33 а) - площадь сечения вертикальной стенки двутавровой балки.