|
ВЕРНУТЬСЯ |
НА ГЛАВНУЮ |
ДАЛЕЕ |
|
Раздел девятый. СТАТИЧЕСКИЙ РАСЧЕТ СТРОИТЕЛЬНЫХ ЭЛЕМЕНТОВ ГИДРОМЕТРИЧЕСКИХ
СООРУЖЕНИЙ ГЛАВА 35. Расчет элементов строительных конструкции, подверженных различным видам деформации |
||
|
35.4. Поперечный изгиб 35.4.2. Построение эпюр изгибающих моментов и поперечных сил |
|
Как известно (см. п. 8.2.3), внутренние силы являются одним из факторов,
определяющих появляющиеся в строительном элементе напряжения, а
следовательно, и его прочность. Поэтому при подборе сечения конкретной
балки необходимо знать, какие в ней действуют внутренние силы и
каково их значение. Для решения этой задачи применим неоднократно
использованный нами метод сечений.
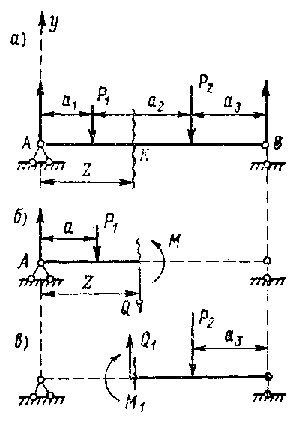
Разрежем балку (рис. 9.27 а) на расстоянии Z от левой опоры; отбросим правую часть и заменим ее действие на левую часть внутренними силами. Известно, что любую систему сил на плоскости можно заменить одной силой, приложенной в произвольно выбранной точке, и парой сил. Заменим отброшенную правую часть силой Q, приложенной в сечении, и парой сил с моментом М (рис. 9.27 6).
Из условия равновесия левой части балки имеем: откуда Таким образом, сила Q численно ра вна алгебраической сумме внешних сил, действующих по одну сторону от сечения. Сила Q характеризует стремление левой части балки сдвинуть правую часть вверх (или вниз) и называется поперечной, или перерезывающей силой. В более общем случае нагружения балки, если внешние силы направлены под углом к продольной оси балки, при вычислении Q берется сумма их проекций на ось у. Возьмем сумму моментов относительно точки К, через которую проходит сечение: откуда Таким образом, изгибающий момент М в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, приложенных по одну сторону от сечения относительно той точки продольной оси балки, через которую проходит рассматриваемое сечение. Момент М выражает стремление левой части балки повернуть правую часть вокруг центра сечения. Изгибающий момент и поперечную силу можно определить так же, рассматривая не левую, а правую часть балки. При этом метод определения Q и М сохраняется. Установим следующее правило для определения знаков изгибающего момента и поперечной силы: изгибающий момент будем считать положительным, если балка изгибается выпуклостью вниз; если сумма проекций внешних сил дает составляющую, направленную вертикально вверх, то Q - положительна. Для того чтобы произвести расчет балки на изгиб, необходимо знать максимальные значения М и Q, а так как они зависят от положения на балке сечения, для которого они рассчитываются, то возникает необходимость выяснения закона изменения изгибающего момента и поперечной силы по длине балки. С этой целью обычно строят так называемые эпюры М и Q. Ось абсцисс эпюры (графика) М проводят параллельно оси балки. Для ряда сечений вычисляют значения изгибающих моментов и откладывают их в масштабе по перпендикуляру к оси; полученные точки соединяют. При этом положительные значения М откладываются вниз от оси. Аналогично строят эпюру Q, откладывая положительные значения поперечной силы вверх по оси, а отрицательные - вниз. При расчете и построении эпюр рекомендуется придерживаться следующего порядка:
Проиллюстрируем
сказанное несколькими примерами. загруженной равномерно распределенной
нагрузкой интенсивностью q кН/м погонной длины балки (рис.
9.28).
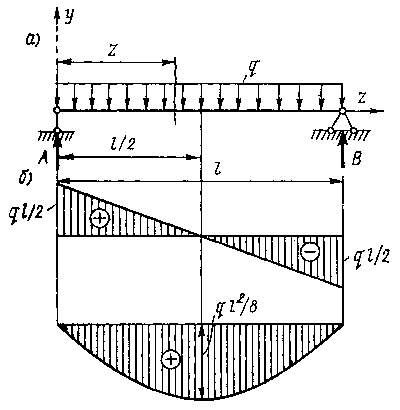
Пример 1. Построим эпюры Ввиду симметрии загрузки балки опорные реакции равны друг другу, а так как сумма реакций равна всей нагрузке, то
т. е. в простейших случаях опорные реакции определяются и без составления уравнений равновесия. По характеру загруженности балка состоит всего из одного участка, равного длине балки. В пределах этого участка проводим произвольное сечение на расстоянии z от левой опоры. Поперечная сила в этом сечении описывается формулой Получили уравнение прямой линии, которую можно построить по двум точкам, вычислив значения Q на границах участка:
Выбрав масштаб по этим ординатам, строим график (рис. 9.28 б), который и представляет собой эпюру поперечных сил. Изгибающий момент в выбранном сечении определяется по формуле Получили уравнение параболы и теперь придется искать местоположение максимального момента и его значение. Координату т. е. максимальный изгибающий момент будет на середине участка (для симметричной нагрузки это очевидно и так, но мы проделали вычисления с целью иллюстрации всего расчета). Подставив значение
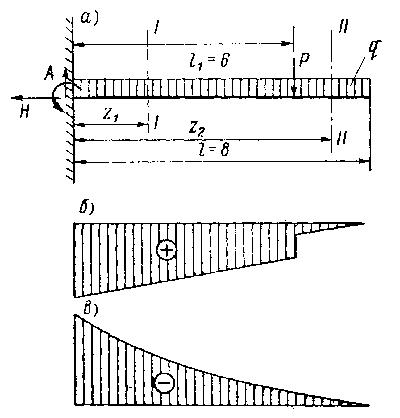
Выбрав масштаб по трем точкам (z = 0, z = l/2, z = l), строим эпюру Обратим внимание на то, что в точке, где момент имеет максимальное значение, поперечная сила равна нулю. Это вытекает и из более общей дифференциальной зависимости , установленной русским инженером Д. И. Журавским. Приведенную зависимость можно использовать для проверки расчетов М и Q. Пример 2. Построим эпюры для консольной балки (балки с одной опорой), загруженной равномерно распределенной нагрузкой и сосредоточенной силой по схеме, изображенной на рис. 9.29.
Для нахождения опорной реакции в опоре типа "заделка" составим три уравнения равновесия: где ql - это равнодействующая распределенной нагрузки; т. е. горизонтальная составляющая опорной реакции равна нулю, чего и следовало ожидать, так как при поперечном изгибе не должно быть сил, действующих вдоль оси балки; В соответствии с характером загруженности устанавливаем, что балка имеет два различных участка, для которых должны быть составлены аналитические выражения Рассмотрим сначала построение эпюры поперечных сил. Для первого участка (сечение I - I) имеем: Для второго участка (сечение II - II) поперечная сила равна: Из полученных уравнений видно, что поперечная сила изменяется по закону прямой и ее эпюру легко построить по значениям Q, вычисленным в трех точках (рис. 9.29 б). Обратим внимание на то, что в точке z = 6, где приложена сосредоточенная нагрузка P, поперечная сила делает скачок, равный этой внешней силе. Произведем вычисления для построения эпюры моментов. Для первого участка (сечение I - I) изгибающий момент определяется равенством: (Поскольку на данном участке изгибающий момент меняется не по линейной зависимости, то для более точного построения эпюры можно было бы вычислить значения М еще в нескольких точках в пределах Далее находим изгибающий момент для произвольного сечения, лежащего в пределах второго участка: Закон изменения изгибающего момента представляет собой параболу. Для построения эпюры М найдем местоположение максимума и его значение, продифференцировав и приравняв к нулю последнее уравнение: т. е. изгибающий момент оказался на конце балки, противоположном заделке. Его значение нами уже найдено. Оно равно нулю. (Ясно, что 0 больше чем - 124 кНм.) Теперь строим эпюру моментов (рис. 9.29 в). Сопоставляя эпюры |
|
ВЕРНУТЬСЯ |
НА ГЛАВНУЮ |
В НАЧАЛО |
ДАЛЕЕ |