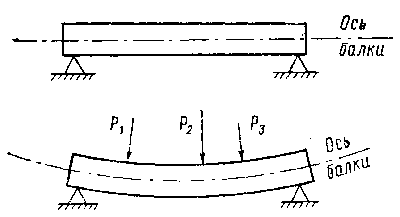
В большинстве сооружений встречаются строительные элементы, работающие на поперечный изгиб. Этот вид деформации возникает под действием сосредоточенной или распределенной нагрузки, направленной по нормали к продольной оси элемента (рис. 9.22), который в таком случае обычно называют балкой.
Для того чтобы балка могла воспринимать нагрузку и передавать ее другим строительным элементам, например, основанию сооружения, она должна иметь соответствующие опоры, в которых, как известно, возникают силы, называемые опорными реакциями или реакциями связей.

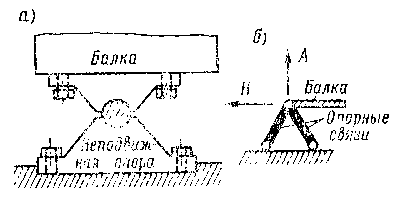
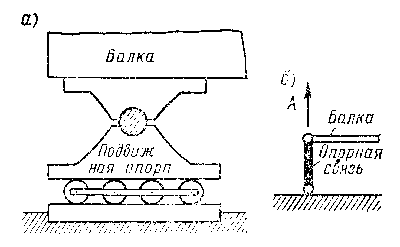
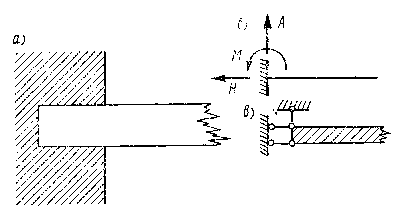
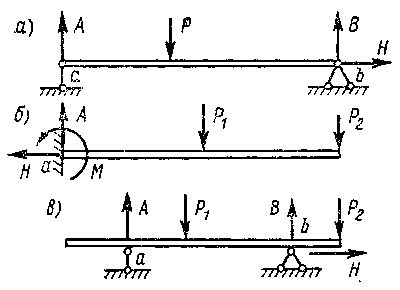
Рис. 9.22. Балка, работающая на поперечный изгиб.

        В строительной практике очень часто встречаются балки, поперечное сечение которых имеет хотя бы одну ось симметрии. Если все силы, в том числе и опорные реакции, лежат в плоскости, совпадающей с осью симметрии сечения, то ось изогнутой балки так же лежит в этой плоскости. Такой изгиб называют плоским, а плоскость, в которой лежат все нагрузки, - силовой. Мы ограничимся рассмотрением именно плоского изгиба.
        При плоском поперечном изгибе в поперечных сечениях балки возникают максимум два внутренних силовых фактора: изгибающий момент и поперечная сила, а нормальная сила при этом равна нулю. Однако в зависимости от способов приложения нагрузки и конструкции опор могут возникать и другие виды изгиба. Отметим один из них, а именно чистый изгиб, характеризующийся тем, что изгибающий момент в поперечных сечениях балки является единственным внутренним силовым фактором.
        Строительной практике известны различные конструкции опор. С точки зрения возникающих в них опорных реакций конструкции опор схематизируют следующим образом.

Шарнирно-неподвижная опора (рис. 9.23 а). Эта опора допускает свободный поворот сечения балки над опорой в одной плоскости относительно оси цилиндрического шарнира, но не дает возможности смещаться ни по вертикали, ни по горизонтали. Схематически шарнирно-неподвижная опора изображается в виде двух стерженьков, шарнирно соединенных с балкой (рис. 9.23 6). Подразумевается, что шарнир не оказывает сопротивления вращению примыкающего к нему сечения балки. В такой опоре возникают две составляющие опорной реакции: А и Н.

Рис.9.23. Шарнирно-неподвижная опора.

Шарнирно-подвижная опора (рис. 9.24 а). Эта опора допускает перемещение в одном направлении, например по горизонтали, и поворот сечения над опорой вокруг шарнира. Схематическое изображение шарнирно-подвижной опоры показано на рис. 9.24 6. Реакция такой опоры А направлена вдоль опорной связи или перпендикулярно плоскости опирания катков.

Рис.9.24. Шарнирно-подвижная опора.

Заделка (рис. 9.25 а). Такая опора не допускает поворота и перемещения по двум направлениям сечения балки, примыкающего к заделке. Схематически заделка изображается так, как показано на рис. 9.25 б. Реакции в заделке состоят из вертикальной силы А, горизонтальной силы Н и момента М.

9.25. Опора-заделка.

Для того чтобы балка могла воспринимать нагрузку, расположенную в одной плоскости, ее необходимо закрепить в этой плоскости с помощью описанных выше связей. Наименьшее число связей, обеспечивающее неподвижность балки по отношению к основанию в одной плоскости, равно трем. Применяют различные варианты прикрепления балки к основанию с помощью рассмотренных выше опор: например, достаточно балку заделать одним концом или закрепить с помощью двух опор (подвижной и неподвижной).
На рис. 9.26 показаны различные типы балок в зависимости от способов прикрепления их к основанию:

Рис. 9.26. Балки с различными типами опор.

простая двухопорная балка (рис. 9.26 а), у которой одна опора подвижная, а другая неподвижная;
балка, заделанная одним концом (рис. 9.26 6);
балка с консолями (рис. 9.26 в).

Встречаются также более сложные типы балок, представляющие собой систему брусьев, соединенных между собой связями.
Мы, несколько упрощая положение, будем считать, что если одна деревянная балка свободно лежит своим концом на другой балке, то между ними образуется шарнирно-подвижная опора, если же балки скреплены между собой болтом или скобами, то опора шарнирно-неподвижная.
Для расчета балки на изгиб надо знать все приложенные к ней силы. Поскольку внешняя нагрузка обычно бывает задана, то возникает проблема определения только опорных реакций. Этот вопрос подробно рассматривается в курсе теоретической механики. Здесь же напомним кратко, что для вычисления величины опорных реакций используются уравнения равновесия, которые для плоской системы сил могут быть записаны в одной из трех следующих форм:

        При вычислении опорных реакций необходимо стремиться так составить уравнения, чтобы в каждое из них входило только одно неизвестное. Этого можно достичь, например, составляя уравнения моментов (вторая форма) относительно опорных точек. Тогда, определив реакции А и В (см. рис. 9.26 а), третье уравнение (сумму проекций сил на ось координат) используют как тождество для проверки полученного решения. Иначе говоря, сумма вертикальных опорных реакций должна равняться сумме всех вертикальных внешних сил.
        Обратим внимание, что в случае плоского поперечного изгиба, который, как отмечалось выше, имеет место при действии внешней нагрузки нормально продольной оси балки, горизонтальные составляющие опорных реакций, независимо от типа опор, равны нулю. Используя приведенные выше уравнения равновесия, можно находить опорные реакции только таких балок, где количество неизвестных реакций не превышает трех. Эти балки называют статически определимыми.
        Встречаются статически неопределимые балки, имеющие число реакций больше числа независимых уравнений равновесия, которые можно составить для их определения. Опорные реакции находятся и в этом случае, однако, более сложными способами, изучение которых выходит за рамки настоящего учебного пособия.