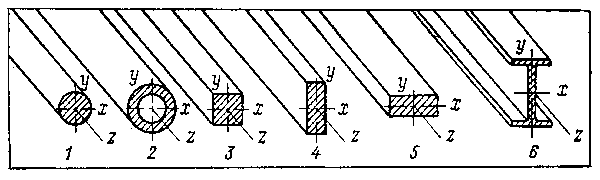
Рассматривая в предыдущих разделах простейшие виды деформаций - осевое растяжение и сжатие, смятие, скалывание - мы выяснили, что их сопротивление действующей силе пропорционально только размерам площади поперечного сечения элемента, на который действует сила. Так, при одинаковой площади сечения, одном и том же материале и одинаковой силе, действующей на каждый из стержней, изображенный на рис. 9.14, в них возникнут равные напряжения.
        Переходя далее к изучению других более сложных видов деформаций (кручение, изгиб, внецентренное сжатие и др.) мы увидим, что в этих случаях сопротивление элемента конструкции внешним силам зависит не только от площади его поперечного сечения, но и от распределения этой площади в плоскости сечения, т. е. от формы сечения.
        Из обыденного опыта ясно, что согнуть стержень 4 в вертикальном направлении труднее, чем стержень 5, а стержень 6 имеет еще большую жесткость, хотя площади сечений всех этих стержней одинаковые (рис. 9.14).

Рис. 9.14. Строительные элементы с поперечными сечениями различной формы.

        Параметрами, характеризующими геометрические свойства различных плоских фигур, кроме площади, являются: статические моменты, моменты инерции, моменты сопротивления и радиусы инерции.
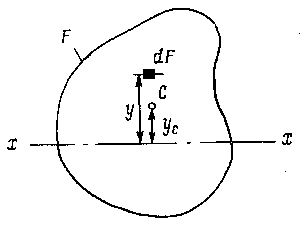
        Статический момент площади. Представим брус с произвольной формой поперечного сечения площадью F, в плоскости которого проведена ось х (рис. 9.15). Выделим элемент площади dF, расположенный на расстоянии у от оси х.. Статическим моментом элементарной площадки 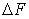, относительно оси х называют произведение этой площадки на ее расстояние до оси:

Рис. 9.15. Схема к определению статического момента сечения.

Статический момент всей площади F относительно оси х равен сумме статических моментов всех элементарных площадок, которые могут быть выделены на рассматриваемой площади:


Если кроме оси х будет проведена еще и ось у, то по аналогии можно записать:


Из теоретической механики известно, что координаты центра тяжести площади фигуры определяют по формулам:

Поэтому

Следовательно, статический момент фигуры площадью F относительно какой-нибудь оси равен произведению площади на расстояние центра тяжести фигуры до этой оси. Размерность статического момента - единица длины в кубе ( , ).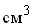
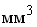        Оси, проходящие через центр тяжести сечения, называют центральными.Если фигура имеет ось симметрии, то последняя всегда проходит через центр тяжести фигуры, т. е. оси симметрии одновременно являются и центральными осями.
        Будем также иметь в виду, что статический момент сложной фигуры относительно некоторой оси равен сумме статических моментов относительно той же оси простых фигур, на которые может быть разбита исходная сложная фигура:


где 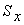- статический момент всей фигуры, a 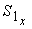, 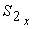и т. д. - статические моменты отдельных частей фигуры.
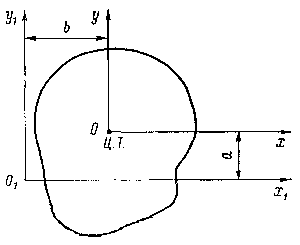
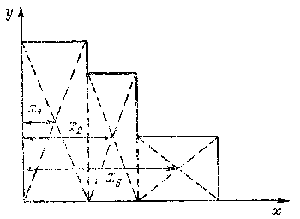
        Отмеченное свойство статического момента в частности используют для нахождения координат центра тяжести несимметричной фигуры, например такой, которая изображена на рис. 9.16.

Рис. 9.16. Схема к определению координат центра тяжести сложной фигуры.

        Для решения этой задачи выберем две оси координат х и у, совпадающие со сторонами фигуры. Разобьем фигуру, все размеры которой должны быть известны, на элементарные части - прямоугольники - координаты центров тяжести которых очевидны, так как эти части симметричны. Составим теперь выражения для вычисления статического момента всей площади, например относительно оси у. Это можно сделать двумя способами:
        а) взять сумму статических моментов отдельных площадей


        б) взять статический момент всей площади


В этих выражениях F - площадь всей фигуры; 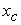- координата ее центра тяжести; 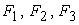- площади отдельных частей фигуры, а 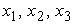- координаты их центров тяжести.
        Приравнивая друг к другу написанные выше формулы, получим уравнение с одной неизвестной :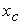


откуда находим координату центра тяжести относительно оси у:


Аналогично этому расстояние центра тяжести фигуры от оси х может быть выражено так:

        Момент инерции. Если элементарные площадки, выделенные в пределах рассматриваемого сечения, будем умножать не на их расстояния до оси х, как при определении статического момента (см. рис. 9.15), а на квадраты расстояний до оси, то получим осевые моменты инерции площадок. Суммируя моменты инерции всех площадок, найдем осевые моменты фигуры в целом:


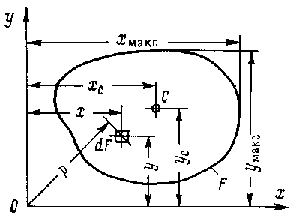
        Составляя интеграл, в котором подынтегральное выражение представляет собой произведение элемента площади на квадрат расстояния до начала координат (рис. 9.17), получим полярный момент инерции:

Рис. 9.17. Схема к определению моментов инерции и моментов сопротивления.

        Отметим еще одну характеристику, в которой площадка dF умножается на произведение координат


Эту величину называют центробежным моментом инерции. Приведенные моменты инерции измеряются в единицах длины" взятой в четвертой степени (, ).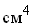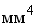
        Осевые и полярные моменты инерции фигуры - величины положительные и не могут быть равными нулю. Центробежный момент инерции в зависимости от положения осей может быть положительным или отрицательным, а также равным нулю. Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называют главными осями инерции и обозначаются 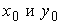. Для симметричной фигуры ось симметрии является и главной осью.
        Осевые моменты инерции, определенные относительно главных осей, имеют максимальное и минимальное значения.
        Так же как и для статического момента, момент инерции сложной фигуры равен сумме моментов инерции образующих ее фигур. Подчеркнем, что сказанное справедливо в том случае, когда все моменты инерции вычисляются относительно одной и той же оси.
        Для моментов инерции существует еще одно правило, часто используемое в расчетах. Применительно к осевым моментам оно "формулируется следующим образом: момент инерции фигуры относительно оси, параллельной центральной, равен моменту инерции относительно центральной оси плюс произведение площади фигуры, на квадрат расстояния между осями (рис. 9.18):

Рис. 9.18. Схема к определению моментов инерции относительно разных осей координат.

Для центробежных моментов инерции соответствующее правило в аналитическом виде выглядит так:


        Для получения значения момента инерции конкретной фигуры в принципе надо решить соответствующий интеграл по площади этой фигуры. Однако с целью облегчения инженерных расчетов такие интегралы для наиболее распространенных форм поперечных сечений строительных элементов уже решены и результаты решений в виде формул представлены в таблицах, одна из которых помещена в приложении 3.
        Кроме того, в ГОСТах на все стандартные профили проката, выпускаемые в нашей стране (уголки, двутавры и др.), даются значения осевых моментов инерции и других геометрических характеристик для каждого типоразмера проката (см. приложение 4).
        Наконец, для сложных по форме сечений моменты инерции определяют, используя изложенные выше два правила: о сложении моментов инерции и о пересчете моментов инерции относительно одних осей на другие оси.
        Момент сопротивления. Осевым моментом сопротивления плоской фигуры относительно какой-либо оси, лежащей в плоскости фигуры, называется частное от деления момента инерции относительно той же оси на расстояние до наиболее удаленной точки фигуры (см. рис. 9.17):


        Полярным моментом сопротивления или моментом сопротивления при кручении плоской фигуры относительно какого-либо центра (полюса), лежащего в плоскости фигуры, называется частное от деления полярного момента инерции относительно того же центра на расстояние от центра до наиболее удаленной точки фигуры:


Моменты сопротивления имеют размерность длины в кубе (, ).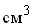
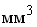        Формулы для расчетов осевых моментов сопротивлений наиболее часто встречающихся фигур приведены в приложении 3, а конкретные значения этой характеристики для профилей стального проката даны в ГОСТах (приложение 4). Отметим, что в отличие от моментов инерции моменты сопротивления складывать нельзя.
        Радиус инерции. Радиусом инерции называется величина, получаемая по формуле


т. е. это квадратный корень из отношения соответствующего осевого момента инерции к площади фигуры. Данная геометрическая характеристика имеет размерность длины.
        Значения радиусов инерции для стального проката даны в ГОСТах (приложение 4). Для квадратного сечения со стороной h радиус инерции относительно оси симметрии, параллельной стороне сечения, находят по формуле


а для круга диаметром d радиус инерции относительно оси, проходящей через центр круга, равен


        Сфера применения рассмотренных выше геометрических характеристик сечений будет раскрыта при изучении видов деформаций, которым посвящены следующие подразделы настоящей главы.