Осевым растяжением (сжатием) кого-либо элемента конструкции, например, прямого бруса, называется деформация, при которой все его волокна, расположенные вдоль оси, получают одинаковое удлинение (укорочение).
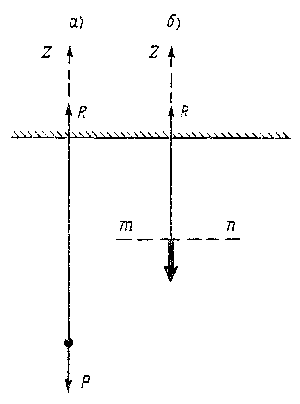
        Прямой брус (или вертикально натянутый канат) испытывает осевое (чистое, центральное) растяжение, если в его поперечных сечениях возникает только один внутренний силовой фактор - продольная сила N, а все остальные внутренние силы равны нулю. Для этого необходимо, чтобы внешние силы, приложенные к брусу по одну сторону от любого его поперечного сечения, были направлены по продольной оси бруса или приводились к равнодействующей, направленной по этой же оси. В частных случаях это могут быть две силы, приложенные по концам бруса и направленные в противоположные стороны (рис. 9.1 а); одна сила, приложенная к брусу, закрепленному на другом конце (рис. 9.1а б); несколько сил, приложенных в различных точках оси бруса (рис. 9.1а б). В последнем случае на отдельных участках бруса может возникнуть растяжение или сжатие в зависимости от направления и величины сил.

Проделаем изложенное выше применительно к канату, на конце которого подвешен груз весом Р (рис. 9.1 а б) (весом самого каната в данном случае пренебрегаем). Направим ось Z по направлению каната вверх. Из условия равновесия каната (сумма проекций всех сил на ось Z должна быть равна нулю) определим величину опорной реакции R


т. е. опорная реакция численно равна нагрузке Р.
        Теперь, когда все внешние силы известны, перейдем к определению внутренних сил, для чего воспользуемся методом сечений. Проводим перпендикулярно оси каната в произвольном месте сечение m-n. Мысленно отбросим нижнюю часть каната и заменим нормальные силы упругости в сечении m-n их равнодействующей N (рис. 9.1 Б б). Из условия равновесия оставшейся верхней части каната следует

        Таким образом, в случае осевого растяжения возникающий в поперечных сечениях элемента внутренний силовой фактор - продольная сила N - численно равна нагрузке, приложенной к элементу.
        Исходя из того, что при осевом растяжении (сжатии) все продольные волокна тела испытывают одинаковое удлинение (укорочение) - это следует из определения данного вида деформаций - можно предположить, что внутренние силы в любом сечении тела (равнодействующей которых является продольная сила N), а также и нормальные напряжения распределяются по поперечному сечению равномерно, т. е. . В таком случае правомерна зависимость

,

(9.1)

где F - площадь сечения.
        Знак напряжения зависит от направления продольной силы N. При растяжении продольная сила направлена от сечения, а напряжение считается положительным, при сжатии - наоборот.

Сжатие считается осевым, если под действием сжимающих сил не происходит изгиба продольной оси тела. В противном случае деформация называется продольным изгибом (см. п. 9.8).

Волокном условно называют последовательный, ряд частиц материала бруса, расположенных по некоторой линии.