Вычисление деформаций и перемещений строительных элементов необходимо для расчетов их на жесткость. В частности, при растяжении какого-либо стержня его длина увеличивается, а поперечные размеры сокращаются, при сжатии, наоборот, длина стержня уменьшается, а поперечные размеры увеличиваются.
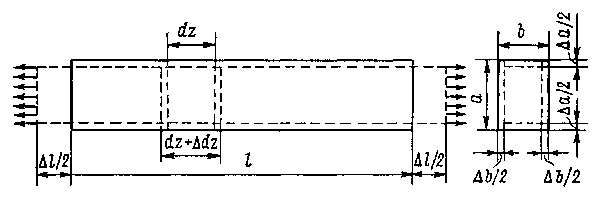
        На рис. 9.1 в пунктиром показан деформированный вид растянутого стержня. Изменение первоначальной длины стержня называется абсолютным удлинением, которое измеряется в единицах длины. Другой мерой продольной деформации является удлинение, отнесенное к единице первоначальной длины стержня. Отношение

(9.2)

называется относительным удлинением. Это отвлеченное число.

Рис. 9.1 в. Деформации тела при осевом растяжении.

        Аналогично находим поперечные деформации в направлении размера а:


и в направлении размера b:


        В последних двух выражениях знак минус поставлен потому, что при растяжении поперечные размеры уменьшаются. Для изотропных материалов поперечные деформации одинаковы, т. е.


Отношение поперечной деформации к продольной, взятое по абсолютному значению при осевом растяжении или сжатии, называют коэффициентом Пуассона

(9.3)

        Для различных материалов значения этого коэффициента лежат в пределах .
        Между напряжениями и деформациями существует зависимость, известная под названием закона Гука. Для осевого растяжения (сжатия) она имеет вид

(9.4)

и может быть сформулирована так: при растяжении (сжатии) нормальное напряжение прямо пропорционально относительному удлинению (укорочению).
        Коэффициент пропорциональности Е между напряжениями и деформациями называется модулем упругости при растяжении (иначе, модулем упругости первого рода) и измеряется в тех же единицах, что и напряжение.
        Модуль упругости для определенного материала (сталь, чугун, резина и пр.) является величиной почти постоянной. При решении большинства практических задач значения модуля упругости можно принимать одинаковыми при растяжении и сжатии и равными:

для стали ; чугуна ; меди ; дерева (вдоль волокон); бетона .

        Закон Гука - один из основных законов в сопротивлении материалов. Прямая пропорциональная зависимость между напряжением и деформацией является простейшим приближенным выражением сложного физического закона и довольно хорошо соблюдается для многих материалов при напряжениях, не превышающих определенного для них предела.
        Подставив в формулу (9.2) значение е из закона Гука и значение а из формулы (9.1), получим:

(9.5)

        Величина EF называется жесткостью стержня при растяжении и сжатии. Жесткость одновременно характеризует физические свойства материала и геометрические размеры сечения. Формула для напряжений (9.1) и закон Гука (9.4) или (9.5) являются основными при расчетах на растяжение и сжатие.
        Пример. При измерении глубины озера счетчик гидрометрической лебедки зафиксировал, что для опускания гидрометрического груза от поверхности воды до дна водоема с барабана лебедки было стравлено 538,0 м каната. Какова истинная глубина озера в пункте измерения с учетом растяжения материала проволочек каната, если его диаметр 4,9 мм, площадь сечения всех проволочек F = 8,5 , масса 100 м погонной длины каната 83,7 кг, масса груза 50 кг.
        Решение. Удлинение каната происходит под действием двух сил: веса груза и веса самого каната. В таком случае деформации (и напряжения) определяют на основе принципа независимости действия сил, т. е. искомые величины находят отдельно для каждой силы, после чего результаты складывают.
        Удлинение материала проволочек каната под действием веса гидрометрического груза легко находится по формуле (9.5). Приведя все параметры к размерностям в системе единиц СИ, получим:


        Растяжение материала проволочек каната под действием собственного веса находится несколько сложнее. Для решения этой задачи учтем, что формула (9.1), выведенная применительно к сосредоточенной нагрузке, в случае нагрузки распределенной (а вес каната является для него именно такой нагрузкой), преобразуется к виду:

(9.6)

где - внутренняя сила в сечении на расстоянии z от точки опоры(подвеса) каната; l - длина каната; р - интенсивность распределенной нагрузки (вес единицы длины каната).
        Для каната

(9.7)

где F - площадь сечения каната; - объемный вес материала, из которого сделан канат. Подставив (9.7) в (9.6), получим


        Напряжения в этом сечении найдем по формуле (9.1):

(9.8)

откуда следует, что напряжения меняются по линейному закону от в нижнем конце каната при z = l, до в верхнем конце (в точке подвеса) при z = 0.
        В рассматриваемом случае теоретическая механика для определения смещения и сечения z дает выражение


из которого с учетом (9.8) следует:

(9.9)

        Таким образом, при z = 0 (точка подвеса) смещение равно нулю, на нижнем конце при z = l смещение будет наибольшим, равным полному удлинению каната

(9.10)

        Умножив числитель и знаменатель формулы (9.10) на F, получим


Выражение равно собственному весу каната G. Поэтому

(9.11)

        Воспользовавшись формулой (9.11) и выразив вес каната в МН, найдем удлинение материала проволочек каната под действием его собственного веса:


        Общее удлинение материала проволочек каната под действием гидрометрического груза и веса самого каната составит


т. е. величину, пренебрегать которой, по-видимому, не стоит. Заметим, что реальное удлинение каната будет еще несколько больше в связи с некоторым спрямлением под нагрузкой закрученных проволочек каната. Величина удлинения за счет этого фактора зависит от конструкции каната (в частности, от способа свивки) и может быть определена только экспериментально.