|
ВЕРНУТЬСЯ |
НА ГЛАВНУЮ |
ДАЛЕЕ |
|
Раздел девятый. СТАТИЧЕСКИЙ РАСЧЕТ СТРОИТЕЛЬНЫХ ЭЛЕМЕНТОВ ГИДРОМЕТРИЧЕСКИХ
СООРУЖЕНИЙ ГЛАВА 34. Основы науки о сопротивлении материалов |
||
|
34.2. Основные понятия
34.2.3. Понятие о напряжении |
Выявив внутренние силы, возникающие в теле при том или ином виде деформации,
еще нельзя говорить об условии прочности рассматриваемого тела, так
как прочность зависит не только от равнодействующей внутренних сил,
но и от материала, образующего тело, и от размеров сечения, к которому
приложена равнодействующая. Для выяснения взаимосвязи между указанными
факторами поступим следующим образом. Разрежем сечением рассматриваемое
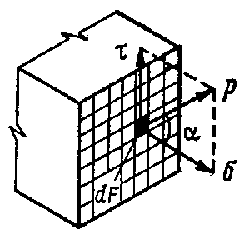
тело и возьмем, например, его левую часть (рис. 8.7).
Разделим
площадь сечения на большое число малых площадок
представляет собой среднее напряжение на данной площадке. Если площадку Таким образом, напряжение - это внутренняя сила, приходящаяся на единицу площади сечения. Единица напряжения Поскольку напряжение есть удельная сила, его можно изображать вектором определенной величины и направления. Напряжение р на выделенной площадке dF в общем случае составляет с нормалью n к этой площадке некоторый угол Такое разложение напряжения на составляющие имеет определенный физический смысл. Действительно, нормальное напряжение возникает тогда, когда частицы материала, находящиеся в рассматриваемом сечении под действием приложенных к телу сил стремятся отдалиться друг от друга или сблизиться в направлении нормали к этому сечению, т. е. при деформации растяжения или сжатия. Касательные напряжения связаны со сдвигом частиц материала по плоскости сечения. Поэтому их называют еще напряжениями сдвига. Каждый материал может оказывать сопротивление внешним силам лишь до того момента, пока напряжение не достигнет некоторого определенного, свойственного данному материалу значения, после чего этот материал разрушается. Такая величина напряжения называется пределом прочности или временным сопротивлением. Его численное значение находят лабораторным способом при испытании различных материалов. |
|
ВЕРНУТЬСЯ |
НА ГЛАВНУЮ |
В НАЧАЛО |
ДАЛЕЕ |