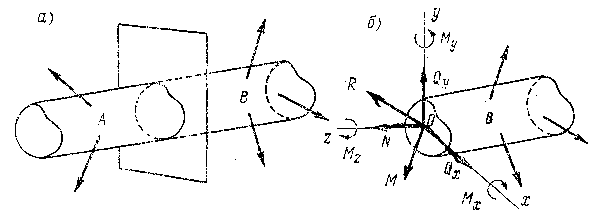
В сопротивлении материалов силы классифицируют по разным признакам. Прежде всего, выделяют силы внутренние и внешние.
        Внутренние силы по своей природе представляют собой взаимодействие частиц тела, обеспечивающее его целостность. Пока на тело внешние силы не действуют, внутренние силы не проявляют себя видимым образом. Как только к телу прикладывают внешние силы, внутренние силы начинают оказывать сопротивление деформированию тела. Деформация упругого тела продолжается до тех пор, пока внутренние силы не уравновесят конечные внешние силы.
        С увеличением внешних сил растут и внутренние. При этом увеличение внутренних сил для каждого материала может происходить только до известного предела, характерного для этого материала. Внешние силы могут оказаться настолько большими, что внутренние силы тела при данных его размерах не смогут их уравновесить. В этом случае тело разрушится.
        Для расчета конструкций на прочность необходимо уметь находить внутренние силы по заданным внешним силам (нагрузкам). Чтобы численно установить внутренние силы, возникающие при той или иной деформации тела, пользуются методом сечений, который сводится к четырем действиям:

1. разрезают (мысленно) тело (рис. 8.1) плоскостью в том месте, где нужно определить внутренние силы;
2. отбрасывают любую отрезанную часть тела (например А);
3. действие отброшенной части на оставшуюся заменяют внутренними силами, чтобы рассматриваемая часть продолжала оставаться в равновесии;
4. для оставшейся части составляют известные из статики уравнения равновесия и из них находят внутренние силы, которые в рассматриваемом сечении являются как бы обычными внешними силами (потому, что другая часть тела в этом сечении отброшена).

Рис. 8.1. Схема применения метода сечений к строительному элементу.

        Однако распределение внутренних сил по сечению методами статики найти невозможно. Зато известно, что любую систему сил можно привести к ее статическому эквиваленту в виде одной силы R (главный вектор) и одной пары М (главный момент). В свою очередь главный вектор и главный момент могут быть разложены по трем осям координат: для вектора это будут силы а для главного момента - моменты (рис. 8.1 б).
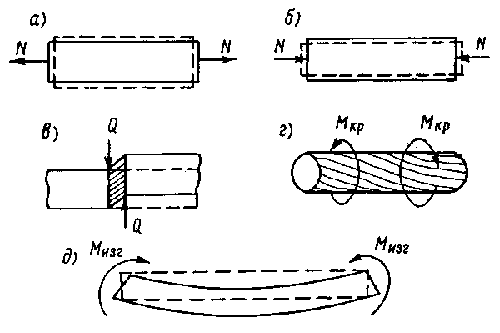
        Полученные таким образом величины представляют собой компоненты внутренних сил, которые принято называть внутренними силовыми факторами, или просто внутренними силами. Каждая из этих сил имеет свое название: силу N, приложенную перпендикулярно сечению, называют нормальной силой; силы перпендикулярные продольной оси тела, - поперечными силами. Моменты называют изгибающими, а - крутящим моментом.
        Чтобы вычислить указанные выше силовые факторы, достаточно написать шесть уравнений равновесия, применяя их к одной из отсеченных частей тела:


        Из трех первых уравнений (представляющих собой суммы проекций всех сил на оси координат) могут быть вычислены силы . Для определения изгибающих и крутящего моментов используются три последних уравнения, являющихся суммами моментов сил относительно соответствующих осей координат.
        При сложных нагрузках, действующих на строительный элемент, в его поперечных сечениях могут одновременно возникать все шесть компонентов внутренних сил. Однако чаще встречают более простые комбинации нагрузок, приводящие к возникновению только какого-либо одного или двух-трех внутренних силовых факторов.
        Отметим, что каждый из силовых факторов связан с определенным видом деформации. Простейшие из них следующие.
        1. Растяжение (сжатие) имеет место в том случае, когда под действием внешних сил, приложенных к рассматриваемой части тела, в его сечении возникает только нормальная сила N, а остальные внутренние силы равны нулю. Деформация здесь заключается в том, что длина элемента увеличивается или уменьшается, т. е. он испытывает или растяжение (рис. 8.2 а), или сжатие (рис. 8.2 б), но при этом продольная ось элемента остается прямой. Так работают, например, канаты, в ряде случаев болты и т. п.

Рис. 8.2. Виды деформаций. а - растяжение; б - сжатие; в - сдвиг (срез); г - кручение; д - поперечный изгиб.

        2. Сдвиг. Действующие в сечении элемента внутренние силы приводятся только к равнодействующей (рис. 8.2 в), равной сумме проекций на ось у всех внешних сил, расположенных по одну сторону от рассматриваемого сечения. На сдвиг работают, например, заклепки, болты, деревянные элементы, соединяемые врубкой, и др.
        3. Кручение. Действующие в сечении тела внутренние силы приводятся только к моменту относительно оси z. При кручении ось элемента остается прямолинейной, а образующие превращаются в винтовые линии (рис. 8.2 г). На кручение работают валы, вороты и т. п.
        4. Изгиб. Действующие в сечении тела внутренние силы приводятся только к моменту относительно оси х, равному сумме моментов всех внешних сил, расположенных по одну сторону от сечения относительно той же оси. В этом случае стержень испытывает деформацию изгиба в вертикальной плоскости (рис. 8.2 д). При изгибе ось тела искривляется, а деформация представляет собой комбинацию растяжения (в нижней части элемента) и сжатия (в верхней части).
        Деформации могут быть сложными, состоящими из нескольких простых деформаций, например, растяжение с кручением, изгиб с кручением, изгиб со сдвигом и пр.
       Далее в пп. 9.1-9.6 будет рассмотрен расчет элементов, подверженных наиболее простым видам деформаций (растяжение, сжатие, сдвиг, кручение, изгиб), а затем перейдем к изучению более сложных случаев. Внешние силы, действующие на конструкцию, называют нагрузками. К внешним силам также относятся реакции связей, наложенных на конструкцию, или опорные реакции. Под внешними силами будем понимать такие, которые приложены к телу извне, со стороны других тел. Так, действие гидрометрического груза на канат, действие людей на настил мостика и другие являются примерами действия внешних сил.
       Классификацию внешних сил производят по нескольким признакам. По способу приложения различают силы сосредоточенные и распределенные. Сосредоточенные силы передаются на элементы сооружения через небольшие площадки и условно считают, что они приложены в точке. К числу таких сил относится, например, давление гидрометрической лебедки на мост. Единицей измерения сосредоточенных сил в обязательной к применению в настоящее время международной системе единиц СИ является ньютон (Н) и кратные ему единицы: килоньютон , меганьютон и др. В широко распространенной технической литературе прежних лет изданий единицами измерения сосредоточенных сил на основе системы МКГСС были тонна-сила (тc) и килограмм-сила (кгс). Между старыми и новыми единицами существует зависимость:


Распределенные нагрузки передаются на сооружение через определенную площадь и измеряются в единицах силы, отнесенной к единице площади - (в старых единицах - ; ; ). К числу таких нагрузок относятся давление снега на кровлю, давление воды на щит водослива с тонкой стенкой и т. п. При расчете многих элементов конструкции распределенную на площадь нагрузку, как показано на рис. 8.3 а, заменяют нагрузкой, которая относится к единице длины элемента (балки).

Рис. 8.3. Нагрузки, действующие на единицу площади (а) и единицу длины (б) строительного элемента.

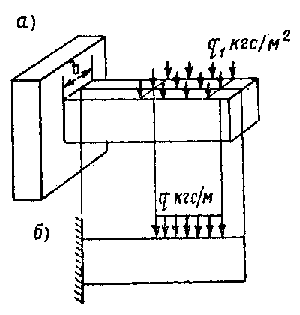
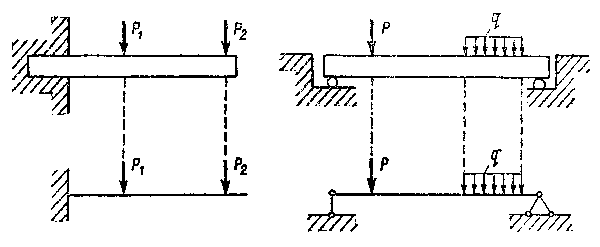
        В этом случае интенсивность нагрузки на единицу длины определяется произведением интенсивности распределенной нагрузки на ширину балки b и поэтому измеряется в единицах силы, отнесенной к единице длины, например Н/м (тс/м).


       По продолжительности действия на сооружение различают нагрузки постоянные и временные. Постоянной называется нагрузка, которая действует непрерывно в течение всего срока службы сооружения, например собственный вес конструкции. Временная нагрузка имеет ограниченную продолжительность действия, например, вес снега и т. п. Заметим, что в сопротивлении материалов собственный вес объемных элементов считается силой сосредоточенной, приложенной в центре тяжести объема, а собственный вес удлиненных элементов (балок) считают распределенным вдоль продольной оси элемента.
       Для того чтобы произвести расчет какого-либо сооружения, сначала необходимо составить так называемую расчетную схему и уже для нее производить все необходимые вычисления. Так, на рис. 8.4 показаны две реальные балки (вверху) и соответствующие им расчетные схемы (внизу). Схематически каждая балка изображается в виде одной осевой линии с идеализированными опорами. При составлении расчетных схем допускаются некоторые отступления от действительных условий работы конструкции. Считается, например, что свободно лежащая балка закреплена на концах шарнирами, в которых нет трения; нагрузка, действующая на балку, передается на ось.

Рис. 8.4. Балки (вверху) и их расчетные схемы (внизу).

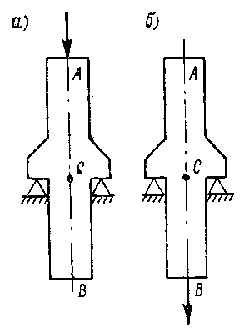
        При составлении расчетных схем необходимо иметь в виду, что некоторые правила теоретической механики применять нельзя. Так обстоит дело с переносом сил по линии их действия и с заменой сил их равнодействующей. Поясним это на примерах. На рис. 8.5, а показан стержень с силой, приложенной в точке А наверху. Если эту силу перенести по прямой в точку В (рис. 8.5 б), то равновесие стержня не нарушится, реакция в точках опоры не изменится, но зато работа стержня резко изменится. В первом случае на участке АС стержень испытывает сжатие, а нижняя часть стержня не нагружена. Во втором случае верхняя часть" стержня не нагружена, а нижняя часть испытывает растяжение. Перенос силы по линии ее действия резко изменил характер работы стержня и поэтому является недопустимым.

Рис. 8.5. Недопустимый перенос силы при составлении расчетной схемы.

        Приведем второй пример. Изучая равновесие тела, можно группу приложенных сил заменять ее равнодействующей и, наоборот, равнодействующую можно разлагать на составляющие. Если речь идет об определении перемещений, то этого делать нельзя. Так, например, на рис. 8.6 а показана балка с тремя равными силами. Замена этих сил их равнодействующей, как это показано на рис. 8.6 б, резко изменяет форму изгиба балки, вместе с тем при определении опорных реакций такая замена в данном случае не приведет к ошибке. Рис. 8.6. Недопустимое сложение сил при определении перемещений.         При расчете сложных инженерных сооружений составление расчетной схемы требует от проектировщика большого искусства.