        Гидродинамическая сетка строится либо по теоретическим решениям, либо экспериментально.
        Современная теория фильтрации под гидротехническими сооружениями разработана акад. Н. Н. Павловским. Однако теоретическое решение задачи движения воды в грунте основания плотин пока еще получено для немногих практических случаев и то большими ограничительными предпосылками. Основной предпосылкой является предположение о совершенной однородности грунта или породы, в которых происходит движение воды; воду считают несжимаемой, силы инерции пренебрежимо малыми, а само движение установившимся, непрерывным и ламинарным.
        Движение плоского грунтового потока через некоторый контур в силу неразрывности жидкости должно удовлетворять уравнению Лапласа и закону Дарси:

(4.12)

(4.13)

где h - пьезометрический напор в точке с координатами х и у; k - коэффициент фильтрац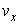ии;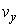

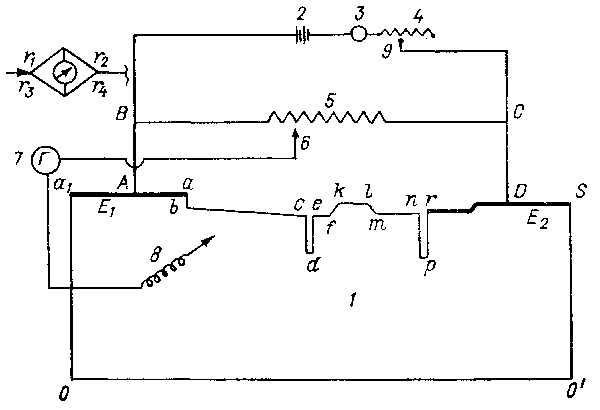
- проекции скорости v на оси х и у.
        Совместное решение уравнений (4.12) и (4.13) представляет даже для сравнительно простых фильтрационных контуров весьма сложную математическую задачу. Удалось получить решение для плотин с плоской подошвой без вертикальных преград в основании, с одной вертикальной преградой (шпунтом, зубом), с несколькими вертикальными преградами (с введением в решение ряда дополнительных ограничений).
        Теоретическое решение дает возможность построить точную картину движения воды под сооружением, т. е. определить в любой точке давление, скорость течения, а также расход фильтрации через то или иное сечение основания.
        Заметим, что, как следует из уравнения (4.12), при однородных грунтах положение линий равного пьезометрического напора не зависит от коэффициента фильтрации грунта k, т. е. при данном подземном контуре сооружения гидродинамическая сетка будет одной и той же как для песка, так и для глины или любого другого грунта (скорости и расходы фильтрационного потока, разумеется, будут зависеть от коэффициента фильтрации).
        В связи с отмеченными выше ограниченными возможностями теоретического метода на практике для построения гидродинамической сетки движения чаще всего пользуются лабораторным методом электрогидродинамических аналогий (ЭГДА). Этот метод был разработан Н. Н. Павловским и основан на том, что движение электрического тока по проводнику подчиняется тем же законам, что и движение фильтрационного потока в грунте. В приборе ЭГДА, используемом для реализации метода, грунт заменяют слоем электропроводящей массы - тонким листом из станиоля, электропроводящей бумагой, жидким электролитом и тому подобным материалом, поток воды - электрическим током, напор воды - электродвижущей силой. Схема прибора представлена на рис. 4.4.

Рис. 4.4. Схема прибора ЭГДА.

Плоский проводник 00'S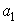

представляет грунт основания плотины. Подземный контур плотины вырезают из проводника например, по ломаной abс...рr. Линии cde и nрr изображают шпунтовые ряды. Верхний бьеф представлен медной шиной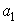

а, нижний бьеф - шиной rDS. Шины соединены с источником эл троэнергин 2. В электрическую цепь включены амперметр 3, реостат 4, провода 9CD и 2ВА и проводник 1. На шинах поддерживают постоянную разность потенциалов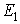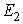

= Е, соответствующую напору воды

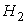= Н. При этом величина Е принимается за единицу (следовательно, Н = 1). В точках В и С в цепь включен калиброванный реохорд 5. Для определения потенциала в любой точке проводника 1 служит игла 8, включенная в электрическую цепь через подвижной контакт 6 и гальванометр 7. Система проводников прибора образует известный из физики мостик Уетстона, причем одна его ветвь будет BA1DC, а другая В5С. Средней соединительной перемычкой мостика служит цепь 8 - 7 - 6, т. е. игла - гальванометр - контакт.
Работа на приборе ЭГДА заключается в следующем. Шкалу реохорда делят на число n, соответствующее требуемому количеству полос напоров (обычно 15 - 20). Далее, присоединяя последовательно подвижной контакт к делениям реохорда 1/n, 2/n, 3/n и т. д., ищут иглой точки на проводнике при нулевом показании гальванометра. Соединяя найденные точки плавными линиями, получим эквипотенциали, проведенные через 1/nЕ или 1/nН, а линии токов строим от руки, соблюдая ортогональность пересечения их с эквипотенциалями и добиваясь сетки, состоящей из криволинейных квадратов. После построения гидродинамической сетки движения дальнейшие вычисления производят, как указано выше.
В настоящее время метод ЭГДА получил широкое распространение при производстве фильтрационных расчетов, а используемое для его реализации лабораторное оборудование стало значительно совершеннее и позволяет решать более сложные и более приближенные к практическим условиям задачи. Имеются установки, моделирующие фильтрацию в слоистых грунтах (с различными коэффициентами фильтрации), неустановившееся движение грунтовых вод, а также пространственные фильтрационные потоки.