|
ВЕРНУТЬСЯ |
НА ГЛАВНУЮ |
ДАЛЕЕ |
| Раздел
первый. ПЛОТИНЫ ГЛАВА 4. Фильтрация воды под плотинами |
||
|
4.3. Расчет элементов фильтрационного потока в мягких грунтах по гидродинамической сетке 4.3.1. Описание гидродинамической сетки |
|
Скорость и расход фильтрационного потока, а также уточненные значения фильтрационного противодавления можно получить на основе построения сетки фильтрации, или гидродинамической сетки. Эта сетка представляет собой семейство двух систем кривых, пересекающихся между собой под прямым углом, — линий равных пьезометрических напоров (эквипотенциалей) при  Н = const и линий
токов, т. е. траекторий движения частиц воды. Н = const и линий
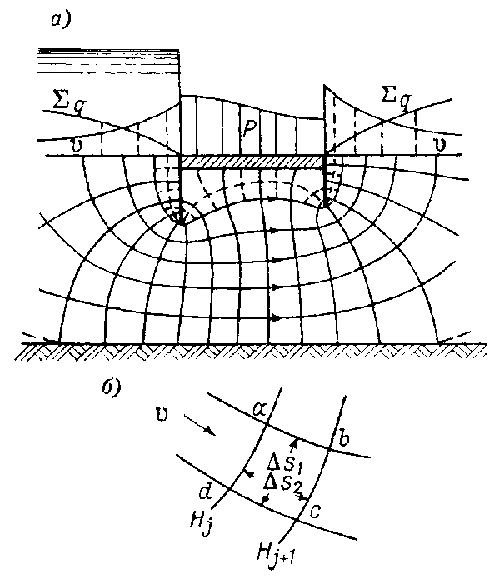
токов, т. е. траекторий движения частиц воды.На рис. 4.3 представлена гидродинамическая сетка движения грунтового потока для двухшпунтового подземного контура. Здесь напор Н разбит на 15 частей и падение напора между двумя соседними эквипотенциалями составляет Н : n = 1/15 Н. Площадь между двумя соседними эквипотенциалями называют полосой напора, а площадь между двумя соседними линиями тока - лентой расхода. Здесь принято m = 6 лент расхода. На входе фильтрационного потока и выходе его в нижний бьеф построены эпюры скоростей v и расходов q, а против плотины - эпюра фильтрационного противодавления р, показывающая нелинейное падение напора по длине.
Выделим в крупном масштабе элемент сетки движения, как показано на рис. 4.3 б. Разность напора между эквипотенциалями 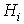 и и  Н = Н
: n, где n - принятое число полос напора. Средняя
скорость движения потока по ленте расхода, согласно закону Дарси,
составит Н = Н
: n, где n - принятое число полос напора. Средняя
скорость движения потока по ленте расхода, согласно закону Дарси,
составит
где 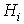 и
и 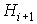 в рассматриваемом криволинейном
прямоугольнике. Из этого выражения видно, что скорость обратно пропорциональна
величине в рассматриваемом криволинейном
прямоугольнике. Из этого выражения видно, что скорость обратно пропорциональна
величине 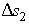 , а так как последняя
увеличивается с расстоянием от основания плотины, то скорости фильтрации
будут уменьшаться в этом же направлении. , а так как последняя
увеличивается с расстоянием от основания плотины, то скорости фильтрации
будут уменьшаться в этом же направлении.
Расход фильтрационного потока через выделенный прямоугольник сетки (т. е. по ленте расхода) на 1 м погонной длины пластины составит
где 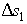 - среднее расстояние между
двумя линиями токов, а 1 - ширина потока из плоскости чертежа. Подставляя
в q значение v получим - среднее расстояние между
двумя линиями токов, а 1 - ширина потока из плоскости чертежа. Подставляя
в q значение v получим
Из этого выражения видно, что если 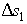 =
= 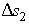 , т. е. если разбивать поле
фильтрационного потока на криволинейные квадраты, то , т. е. если разбивать поле
фильтрационного потока на криволинейные квадраты, то
Для получения полного фильтрационного расхода под плотиной надо помножить расход Q на длину плотины. |
|
ВЕРНУТЬСЯ |
НА ГЛАВНУЮ |
В НАЧАЛО |
ДАЛЕЕ |