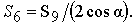|
Для определения усилий в стержнях фермы необходимо знать все действующие
на ферму внешние силы, среди которых, как известно, выделяют нагрузки
и опорные реакции.
Нагрузки задаются условиями
задачи, а опорные реакции вычисляются совершенно так же, как для
балок (см. п. 9.6.1), т. е. на основе уравнений равновесия.
После определения всех
внешних сил приступают к расчету усилий в стержнях фермы. Это можно
делать одним из трех методов:
- методом вырезания узлов;
- методом сквозных сечений (или методом моментных
точек);
- графическим методом (построением диаграммы
Максвелла-Кремоны).
Метод вырезания узлов состоит в том, что усилия в стержнях
любого узла фермы (рис. 10.1 а) определяют при рассмотрении равновесия
только этого узла. Так как все стержни любого узла пересекаются
в одной точке, то усилия, направленные вдоль этих стержней, образуют
систему сходящихся сил. Для сходящихся сил каждого узла фермы можно
составить по два уравнения равновесия и из них найти неизвестные
усилия. Порядок вычисления такой.
На схеме фермы все узлы
обозначают буквами, а все стержни - цифрами. Поочередно вырезают
все узлы фермы и вычерчивают их силовые схемы (рис. 10.1 б), обозначая
стрелками усилия в перерезанных стержнях и внешние силы, приложенные
к данному узлу. Усилия изображают направлениями от узла, т. е. считают,
что все стержни растянуты.
В центр каждого узла
помещают начало осей координат, составляют уравнения равновесия
для сходящихся в узле сил 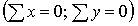 и
находят неизвестные усилия. Если при вычислении усилие получится
с отрицательным знаком, значит оно направлено в противоположную
сторону, т. е. не от узла, а к узлу и, следовательно, соответствующий
стержень не растянут, а сжат. и
находят неизвестные усилия. Если при вычислении усилие получится
с отрицательным знаком, значит оно направлено в противоположную
сторону, т. е. не от узла, а к узлу и, следовательно, соответствующий
стержень не растянут, а сжат.
Порядок вырезания узлов
должен быть таким, чтобы в каждый последовательно рассматриваемый
узел входили только два стержня, усилия в которых неизвестны.
Так, для фермы, изображенной
на рис. 10.1, расчеты можно начинать с узла А (не известны
усилия 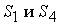 ,
а опорные реакции известны ,
а опорные реакции известны 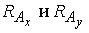 )
или с узла В (не известны усилия )
или с узла В (не известны усилия 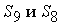 ).
Во всех остальных узлах неизвестных усилий пока еще больше двух. ).
Во всех остальных узлах неизвестных усилий пока еще больше двух.
Напишем уравнение равновесия
для узла В:
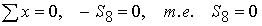 (стержень не работает);
(стержень не работает);
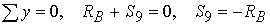 (стержень сжат). (стержень сжат). |
Теперь можно перейти
не только к узлу А, но и к узлу D, так как усилие
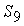 мы уже нашли. Напишем уравнение
равновесия для узла D: мы уже нашли. Напишем уравнение
равновесия для узла D:
В последнее уравнение подставим 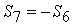 и решим его относительно
и решим его относительно 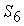 : :
Так, переходя от узла к узлу, найдем усилия во всех стержнях фермы.
Метод сквозных сечений,
или моментных точек, основан на условии, что любая часть фермы находится
в равновесии, если вся ферма находится в равновесии. Реализация
этого метода осуществляется следующим образом.
Определив опорные реакции,
мысленно разрезают ферму (рис. 10.2), проводя сечения по ее стержням
(но не по узлам), и составляют уравнения равновесия для любой части
фермы, лежащей по одну сторону от рассматриваемого сечения 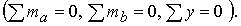 При
этом учитываются: внешние силы (нагрузки) и опорные реакции, приложенные
в рассматриваемой части фермы, и усилия в стержнях, перерезанных
данным сечением. При
этом учитываются: внешние силы (нагрузки) и опорные реакции, приложенные
в рассматриваемой части фермы, и усилия в стержнях, перерезанных
данным сечением.
Сечения необходимо проводить
так, чтобы каждое из них перерезало не более трех стержней с неизвестными
усилиями. В качестве точек, относительно которых составляются уравнения
моментов, удобно выбирать узлы фермы, где пересекаются два стержня
с усилиями, которые надо определить. Тогда моменты этих двух усилий
оказываются равными нулю, а третье искомое усилие легко находится
из одного уравнения. Например, на рис. 10.2 в для определения усилия
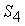 моменты всех сил, лежащих слева
от сечения II-II, вычисляют относительно точки С. В этом
случае обращаются в ноль моменты от усилий моменты всех сил, лежащих слева
от сечения II-II, вычисляют относительно точки С. В этом
случае обращаются в ноль моменты от усилий 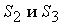 и из одного составленного уравнения находим одно неизвестное усилие
и из одного составленного уравнения находим одно неизвестное усилие
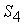 . Для
вычисления усилий в других стержнях выбирают другую моментную точку
или приравнивают нулю сумму проекций всех сил на одну из осей координат. . Для
вычисления усилий в других стержнях выбирают другую моментную точку
или приравнивают нулю сумму проекций всех сил на одну из осей координат.
Неизвестные усилия в
перерезанных стержнях принимают направленными от узла (растягивающими).
Если при решении уравнения равновесия ответ получится со знаком
минус, значит усилие в стержне направлено к узлу (стержень сжат).
Обратим внимание на то,
что в случае симметричной фермы я симметрично приложенных к ней
сил усилия в соответствующих стержнях фермы, например 5 и 5', 4
и 4' и т. д., будут одинаковыми. Поэтому в процессе расчета достаточно
выяснить значения и знаки усилий только для половины стержней фермы.
Графический метод
(построение диаграммы Максвелла-Кремоны) рассмотрим на примере конкретной
фермы (рис. 10.3 а), к которой приложена нагрузка F.
Как всегда при расчете
ферм начинают с определения опорных реакций . Затем на схеме фермы,
вычерченной в масштабе (рис. 10.3a), указывают внешние силы и опорные
реакции, причем стрелочки, изображающие силы, обязательно располагаются
вне данной фермы  . Далее производят
разметку фермы, придерживаясь следующей терминологии и правил. . Далее производят
разметку фермы, придерживаясь следующей терминологии и правил.
Части плоскости, ограниченные
внешним контуром фермы и линиями действия приложенных к ней сил,
называют внешними областями. У нашей фермы имеются три внешние
области, которые обозначим заглавными буквами A, В, С. Части
плоскости, расположенные внутри фермы и ограниченные только стержнями,
называют внутренними областями; их обозначим цифрами 1, 2,
3.
Вычерчивание диаграммы
начинается с построения многоугольника внешних сил. Выбирают масштаб
сил и из произвольной точки плоскости откладывают отрезок, соответствующий
величине и направлению какой-то одной из приложенных к ферме сил.
Затем, обходя ферму по часовой стрелке, откладывают в масштабе от
конца уже изображенной силы другой отрезок, параллельный следующей
силе и т. д. Каждую силу на диаграмме обозначают двумя малыми (строчными)
буквами, соответствующими тем большим буквам, какими обозначены
две смежные внешние области, разграниченные линией действия данной
силы. При этом малые буквы на диаграмме ставятся в том порядке,
в каком расположены две смежные внешние области при обходе фермы
по часовой стрелке. В соответствии с изложенным сила F на
диаграмме (рис. 10.3 б) имеет обозначение аb (а на
bа), сила 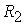 обозначена
bс, а сила обозначена
bс, а сила 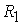 обозначена са. Поскольку ферма находится в равновесии, то
многоугольник внешних сил должен быть замкнутым. У нашего примера
частный случай замкнутого многоугольника - прямая линия.
обозначена са. Поскольку ферма находится в равновесии, то
многоугольник внешних сил должен быть замкнутым. У нашего примера
частный случай замкнутого многоугольника - прямая линия.
Далее, используя как
основу многоугольник внешних сил, пристроим к нему силовые многоугольники
всех узлов фермы, заменяя стержни действующими в них усилиями. На
диаграмме усилия в стержнях обозначаются так же, как и внешние силы,
т. е. по индексам зон (внешних и внутренних), разделяемых соответствующим
стержнем, например, усилие а-1, 2-3, 3-с и т. д.
Для определения усилий
в стержнях надо обойти каждый узел по часовой стрелке и провести
на диаграмме линии, параллельные направлению стержней данного узла.
Отметим, что зонам фермы на диаграмме соответствуют точки. Подчеркнем
также, что обходить можно только тот узел, где на данный момент
сходится не более двух стержней с неизвестными усилиями.
В нашем примере начинать
обход можно с любого опорного узла. Выберем первым левый узел. Зоны
A и С, примыкающие к стержням этого узла, на строящейся
диаграмме уже изображены точками а и с. Для того, чтобы получить
на диаграмме точку 1, соответствующую зоне 1, проведем из точек
а и с линии, параллельные соответствующим стержням а-1, 1-с. На
их пересечении получим точку 1.
Длина отрезков а-1 и
с-1 на диаграмме, переведенная с учетом выбранного масштаба в размерность
сил, дает величину усилий в соответствующих стержнях фермы.
Далее надо обходить другие
узлы фермы. Теперь это можно делать не только для правого опорного
узла, но и для узла нижнего пояса, ближайшего к левой опоре, так
как в нем хотя и сходятся три стержня, но в одном из них с-1 усилие
уже определено. Для названного узла зоны с и 1 на диаграмме изображены
точками с и 1. Требуется отобразить на диаграмме зону 2, т. е. найти
местоположение точки 2. Проведем из точек 1 и с диаграммы линии,
параллельные стержням с-1 и 2-с и на их пересечении получим точку
2. Переходя к следующим узлам, найдем усилия во всех стержнях фермы.
Для определения знака
усилия в стержнях нужно обойти узлы по часовой стрелке, читая на
диаграмме название стержней и замечая по отношению к схеме фермы
направления усилия (первая буква относится к началу вектора, вторая-к
концу). Если усилие направлено к узлу-стержень сжат, если от узла-растянут.
Для примера обойдем верхний узел фермы (рис. 10.3), где приложена
сила F. Начнем со стержня В-3. Читаем на диаграмме соответствующее
усилие в-3: оно направлено к узлу, значит этот стержень сжат. Усилие
в следующем стержне 3-2 направлено от узла (стержень растянут),
далее усилие 2-1 также направлено от узла (соответствующий стержень
растянут) и, наконец, усилие 1-а направлено к узлу, значит последний
стержень сжат.
|
|