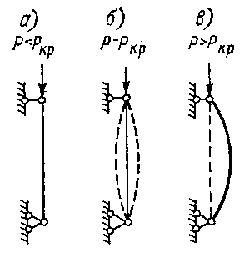будет находиться в устойчивом равновесии. Она не чувствительна к малым возмущениям. Незначительные дополнительные воздействия мало отклоняют стойку от ее прямолинейного состояния и в этой фазе она испытывает простое осевое сжатие. При

прямолинейная форма сжатой стоки неустойчива. Сколь угодно малые случайные воздействия вызовут большие отклонения. Стойка после удаления возмущений останется в изогнутом состоянии под действием продольной силы. Такое состояние называют продольным изгибом. 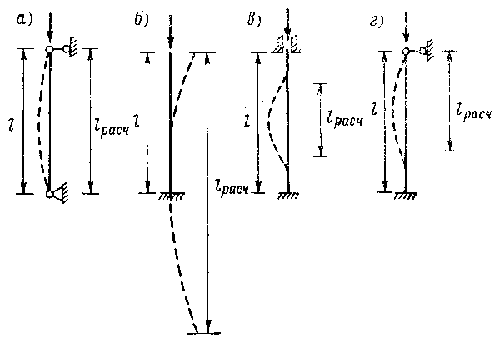Неустойчивая форма равновесия в стойке становится возможной лишь при вполне определенной величине силы, называемой критической силой или критической нагрузкой.
Появление продольного изгиба опасно тем, что при нем происходит очень сильное нарастание прогибов при малом нарастании сжимающей силы. Этот вид деформации возникает, как правило, внезапно, потеря устойчивости начинается задолго до того, как будут исчерпаны прочностные свойства материала, процесс протекает с ускорением и часто приводит к разрушению строительного элемента. Поэтому нагрузки во всех элементах, подверженных сжатию, должны быть меньше критических. Соответственно и рабочие (фактические) напряжения не должны превышать критические

, а те в свою очередь должны быть меньше допускаемых напряжений для данного материала

, т. е.

Формулу для нахождения величины критической силы

в 1744 г. предложил Леонард Эйлер

Здесь Е - модуль упругости; I - минимальный момент инерции сечения;

- расчетная длина сжимаемого элемента, определяемая по зависимости

где l -действительная длина элемента;

- коэффициент, зависящий от типа опор элемента. Его значения находят в соответствии со схемами, изображенными на рис. 9.42:
cхема а: оба конца шарнирно закреплены,

;
схема б: один конец заделан, другой свободен,

;
схема в: оба конца заделаны,

;
схема г: один конец заделан, другой шарнирно закреплен,

Рис. 9.42. Схемы к определению расчетной длины стержня при продольном изгибе.

Однако формула Эйлера действительна только для случаев, когда критическое напряжение

будет меньше предела пропорциональности (см. п. 9.1.3). Поэтому на практике с целью придания универсальности проектированию сжатых элементов их расчет на устойчивость сводят по форме к расчету на осевое сжатие, уменьшив допускаемое напряжение (или расчетное сопротивление). В этом случае отпадает необходимость в непосредственном применении формулы Эйлера.
За основу расчета берутся известные выражения (9.12) и (9.14), которые преобразуют к виду:

где

- коэффициент продольного изгиба

, уменьшающий допускаемое напряжение

(расчетное сопротивление R) при продольном изгибе по сравнению с этими параметрами при осевом сжатии.
Еще удобнее расчетные формулы представить так:

(9.41)

тогда можно пользоваться одними значениями

и R для элементов растянутых, сжатых и подверженных продольному изгибу. Значение коэффициента

зависит от так называемой гибкости стойки

и ее материала. Для некоторых строительных материалов значения

даны в табл. 9.4.

Таблица 9.4

Значения коэффициентов продольного изгиба

Гибкость стержня	Сталь СТ-3, СТ-4	Сталь СТ-5	Чугун, СЧ- 12-28, СЧ- 15-32, СЧ- 18-36	Дерево
0	1,00	1,00	1,00	1,00
10	0,99	0,98	0,97	0,99
20	0,97	0,96	0,91	0,97
30	0,95	0,93	0,81	0,93
40	0,92	0,90	0,69	0,87
50	0,89	0,85	0,57	0,80
60	0,86	0,80	0,44	0,71
70	0,81	0,74	0,34	0,61
80	0,75	0,67	0,26	0,49
90	0,69	0,59	0,20	0,38
100	0,60	0,50	0,16	0,31
110	0,52	0,43	—	0,25
120	0,45	0,37	—	0,22
130	0,40	0,32	—	0,18
140	0,36	0,28	—	0,16
150	0,32	0,25	—	0,14
160	0,29	0,23	—	0,12
170	0,26	0,21	—	0,11
180	0,23	0,19	—	0,10
190	0,21	0,17	—	0,09
200	0,19	0,15	—	0,08
210	0,17	0,14	—	—
220	0,16	0,13	—	—

Гибкость

находят по выражению

(9.42)

где

- минимальный радиус инерции сечения стойки.
Поверочные расчеты элементов, испытывающих продольный изгиб, производят по выражениям (9.41). Для проектных расчетов, т. е. определения площади сечения F, из (9.41) получим

(9.43)

что очень напоминает формулы (9.17), используемые при деформациях осевого растяжения и сжатия. Однако если по (9.17) действительно можно найти F, то по (9.43) этого сделать нельзя, поскольку коэффициент

сам зависит от размеров и формы сечения. Поэтому при деформации продольного изгиба площадь сечения определяют путем подбора. Для этого задают какую-либо форму и размеры поперечного сечения, находят для него

и по формуле (9.41) вычисляют напряжение

. Если оно существенно отличается от допускаемого напряжения

(или расчетного сопротивления R при производстве вычислений по методу предельных состояний), то размеры сечения изменяют в необходимую сторону и повторяют расчет до получения требуемого результата.
Обычно требуется, чтобы разница в указанных напряжениях не превышала 3-5 %.
Пример. Подобрать двутавровое сечение из стали Ст.3 для береговой опоры стоечного типа однотросовой люлечной переправы. Высота опоры 1,5 м, нижний конец ее жестко заделан в фундамент. Расчетная сжимающая сила Р = 0,141 МН. Расчетное сопротивление R = 210

.
Для данного способа закрепления концов стержня

= 2(см. рис. 9.42 б).
В первом приближении выберем двутавр № 16, у которого согласно ГОСТу (приложение 4, табл. 1) F = 20,2

= 1,70 см. Находим

По табл. 9.4 для стали СТ.3 при

Вычисляем напряжение по (9.41):

Так как фактическое напряжение больше расчетного сопротивления, то необходимо увеличить площадь сечения двутавра. Во втором приближении возьмем двутавр № 18 и повторим расчет. Для этого двутавра F = 23,4

= 1,88 см. Тогда

R немного превышает

, что и должно быть. Задача подбора сечения завершена; принимаем двутавр № 18.