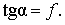|
Раздел девятый. СТАТИЧЕСКИЙ РАСЧЕТ СТРОИТЕЛЬНЫХ ЭЛЕМЕНТОВ ГИДРОМЕТРИЧЕСКИХ
СООРУЖЕНИЙ
ГЛАВА 38. Расчет подпорных стенок, якорей, свай и шпунтов
|
|
|
|
|
|
Перечисленные в названии главы строительные элементы испытывают
непосредственный контакт с грунтами, поэтому конструктивные особенности
этих элементов во многом зависят от свойств грунтов, с которыми
кратко познакомимся ниже.
Некоторые свойства
и характеристики грунтов. Грунты подразделяют на скальные, частицы
которых сцементированы (связаны) в единый монолит, и нескальные,
в которых прочность связей между частицами незначительна и эта связь
существенно меньше прочности самих частиц. К нескальным грунтам
относятся крупнообломочные, песчаные и глинистые.
Характеристики грунта,
необходимые для расчета проектируемого на этом грунте сооружения,
определяют двумя способами. Во-первых, опытным путем в лабораторных
или полевых условиях, такие характеристики называют исходными.
Во-вторых, на основе исходных характеристик по формулам (12.1),
(12.2) и по таблицам (табл. 7.3-7.5) определяют производные
характеристики грунта.
Важнейшими исходными
характеристиками нескальных грунтов являются:
- вид грунта, зависящий от содержания минеральных частиц того
или иного размера;
- гранулометрический состав песчаных грунтов;
- плотность грунта
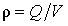 , где
Q - масса образца грунта, г, кг или т; V - объем
образца грунта в естественном состоянии, , где
Q - масса образца грунта, г, кг или т; V - объем
образца грунта в естественном состоянии, 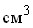 , ,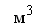 ; ;
- объемный вес сухого грунта
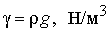 ;
здесь g - ускорение свободного падения, значение которого
в данных расчетах можно принимать равным 10; ;
здесь g - ускорение свободного падения, значение которого
в данных расчетах можно принимать равным 10;
- плотность частиц грунта
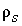 - отношение массы твердой части грунта в сухом состоянии к объему
вытесненной частицами грунта жидкости;
- отношение массы твердой части грунта в сухом состоянии к объему
вытесненной частицами грунта жидкости;
- влажность грунта W (массовая), %:
где 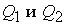 - соответственно масса
влажного и высушенного грунта; - соответственно масса
влажного и высушенного грунта;
- для глинистых грунтов необходимо установить значения двух
влажностей, которые называют границей текучести и границей пластичности
(раскатывания) .
Среди производных характеристик
грунта важнейшими являются:
- пористость, вычисляемая обычно по формуле
- объемный вес взвешенного грунта (находящегося род уровнем
грунтовых вод)
где 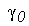 - объемный вес воды. - объемный вес воды.
К другим производным
характеристикам относятся расчетные сопротивления грунтов (табл.
7.4), угол внутреннего трения (табл. 7.3), коэффициент фильтрации
(табл. 7.5) и еще ряд параметров. Поясним смысл такой широко используемой
характеристики, как угол внутреннего трения.
Любой сыпучий грунт,
будучи свободно насыпанным на горизонтальную площадку, образует
откос, крутизна которого зависит от свойств грунта. Рассмотрим откос
идеально сыпучего грунта, т. е. такого, между частицами которого
совершенно отсутствуют силы сцепления, вызываемые коллоидными и
вязкими свойствами частиц грунта.
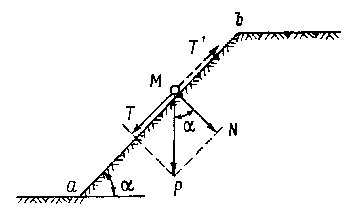
Пусть на этом откосе
(рис. 12.1), свободно лежит твердая частица М. Разложим вес
частицы на две составляющие: нормальную N к линии откоса
аb и касательную Т. Сила Т стремится сдвинуть
частицу к подножию откоса, но ей будет противодействовать сила трения
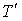 , пропорциональная
нормальному давлению, т. е. , пропорциональная
нормальному давлению, т. е. 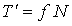 (где f - коэффициент трения).
(где f - коэффициент трения).
| |
Рис. 12.1. Устойчивость частицы грунта на откосе. |
Составим
уравнение равновесия частицы М, спроектировав все силы на
наклонную грань откоса и приравняв их алгебраическую сумму к нулю:
откуда 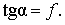
С другой стороны, согласно
закону Кулона, сопротивление сыпучих грунтов сдвигу есть сопротивление
их трению. Характеристикой такого сопротивления является коэффициент
внутреннего трения f, равный тангенсу так называемого угла
внутреннего трения 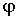 , т.
е. , т.
е.
Из (а) и (б) окончательно получаем:
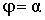 . . |
Таким образом, угол внутреннего трения равен предельному углу откоса
сыпучих грунтов, который еще называют углом естественного откоса.
Понятие об угле естественного
откоса относится только к сухим сыпучим грунтам, а для грунтов связных
глинистых оно теряет всякий смысл, так как у последних в зависимости
от их увлажненности угол откоса может меняться от 0° до 90° и зависит
также от высоты откоса.
Именно из-за такой изменчивости
силы сцепления в связном грунте определение ее величины и учет при
расчете устойчивости откосов и сооружений, удерживающих откосы,
оказывается весьма затруднительным. В дальнейшем удельную силу сцепления
грунта учитывать не будем и для каждого вида грунта станем пользоваться
осредненным значением 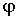 (см.
табл. 7.3). В большинстве случаев такой подход приводит к запасу
устойчивости сооружений. (см.
табл. 7.3). В большинстве случаев такой подход приводит к запасу
устойчивости сооружений.
Подпорные стенки
устраивают в том случае, когда необходимо удержать массив грунта
с откосом, крутизна которого превышает величину, определяемую углом
внутреннего трения и силами сцепления. Типичным примером подпорной
стенки является гранитная или бетонная набережная, удерживающая
практически в вертикальном положении грунт на границе между сушей
и водой.
Здесь мы ограничимся
рассмотрением массивных подпорных стенок, характеризующихся
незначительным заглублением фундамента и большой толщиной. Давлению
грунта такие стенки сопротивляются своей силой тяжести.
На рис. 12.2 изображена
схема подпорной стенки, удерживающей клин земли, имеющий плоскую
поверхность скольжения ВС (допущение Кулона). Устойчивость
такой стенки должна быть проверена по трем показателям:
| |
Рис. 12.2. Подпорная стенка. |
- не произойдет ли сдвига стенки по плоскости
основания АВ;
- не опрокинется ли стенка вокруг ребра A;
- не просядет ли стенка по основанию.
Размеры стенки и материал, из которого она сделана,
считаются заданными. Все расчеты ведут для одного погонного метра
длины стенки (1 м из плоскости чертежа).
Вычисления начинают с
определения основных сил действующих на стенку. Такими силами являются
вес стенки G и активное давление грунта 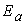 .
Первая из них находится элементарно, а для определения второй необходимо
рассчитать и построить эпюру удельного давления грунта на стенку,
для чего используется формула .
Первая из них находится элементарно, а для определения второй необходимо
рассчитать и построить эпюру удельного давления грунта на стенку,
для чего используется формула
где 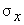 - удельное давление грунта
в точке на глубине - удельное давление грунта
в точке на глубине 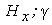 - объемный вес грунта;
- объемный вес грунта; 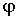 - угол
внутреннего трения. - угол
внутреннего трения.
Выражение (12.3) представляет
собой уравнение прямой линии, поэтому эпюра удельных давлений будет
иметь вид прямоугольного треугольника с максимумом удельного давления
у подошвы стенки (рис. 12.2).
Равнодействующая активного
давления грунта на подпорную стенку 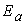 равна площади эпюры
равна площади эпюры
или
Равнодействующая будет
горизонтальна и приложена на одной трети высоты от низа подпорной
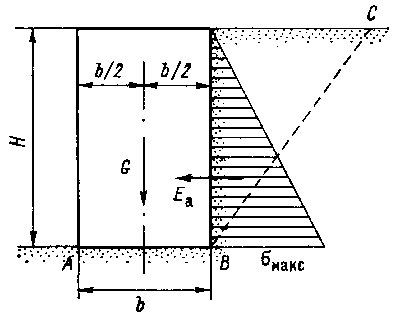
стенки. В случае действия на поверхность грунта сплошной равномерно
распределенной пригрузки q 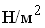 определяем приведенную высоту слоя грунта
определяем приведенную высоту слоя грунта 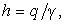 заменяющую ее действие, продолжаем заднюю грань стенки до пересечения
с новой линией засыпки (рис. 12.3) и строим общую треугольную эпюру
давлений.
заменяющую ее действие, продолжаем заднюю грань стенки до пересечения
с новой линией засыпки (рис. 12.3) и строим общую треугольную эпюру
давлений.
| |
Рис. 12.3. Эпюра давления на подпорную стенку при наличии
пригрузки q. |
На подпорную стенку будет
действовать только трапецеидальная заштрихованная часть эпюры давлений
(рис. 12.3). Тогда
или
При вертикальной поверхности
стенки давление 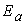 будет действовать
горизонтально в точке, соответствующей высоте расположения центра
тяжести трапецеидальной эпюры давления (рис. 12.3). Однако подпорные
стенки часто имеют заднюю грань наклонной, причем угол наклона будет действовать
горизонтально в точке, соответствующей высоте расположения центра
тяжести трапецеидальной эпюры давления (рис. 12.3). Однако подпорные
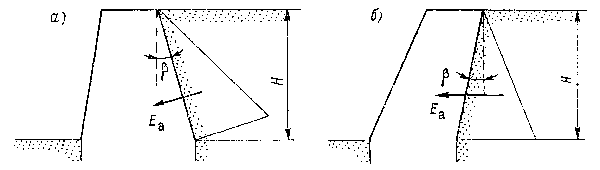
стенки часто имеют заднюю грань наклонной, причем угол наклона 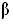 может быть положительным (рис. 12.4 а) или отрицательным (рис. 12.4 б).
может быть положительным (рис. 12.4 а) или отрицательным (рис. 12.4 б).
Наклон задней грани стенки
значительно влияет на величину активного давления, причем по сравнению
с давлением грунта при вертикальной задней грани стенки в первом
случае активное давление будет больше, а во втором - меньше. Расчетные
формулы здесь выглядят так:
- при положительном значении угла
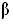 (см. рис. 12.4 а)
(см. рис. 12.4 а)
- при отрицательном значении угла
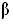 (рис. 12.4 б)
(рис. 12.4 б)
| |
Рис. 12.4. Подпорная стенка с наклонной задней гранью. |
Отметим, что формулы
(12.6) и (12.7), так же как, впрочем, и формула (12.3), выведены
в предположении отсутствия трения между грунтом и стенкой, поэтому
равнодействующая давления должна быть перпендикулярна задней грани
стенки. Это будет соответствовать наблюдаемым явлениям в случае
нисходящей в сторону грунта задней грани стенки (при положительном
значении угла 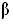 ,
см. рис. 12.4 а). В случае же восходящей в сторону грунта задней
грани стенки (при отрицательном значении угла ,
см. рис. 12.4 а). В случае же восходящей в сторону грунта задней
грани стенки (при отрицательном значении угла 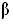 ,
см. рис. 12.4 б) нелогично принимать направление давления с наклоном
вверх, т. е. перпендикулярно задней грани стенки, поэтому рекомендуется
в последнем случае считать направление давления ,
см. рис. 12.4 б) нелогично принимать направление давления с наклоном
вверх, т. е. перпендикулярно задней грани стенки, поэтому рекомендуется
в последнем случае считать направление давления 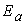 горизонтальным.
горизонтальным.
В случае загрузки горизонтальной
поверхности грунта равномерно распределенной нагрузкой в формулах
(12.6) и (12.7) первый множитель 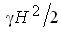 ,
следует заменить выражением ,
следует заменить выражением 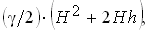 где h - приведенная высота слоя грунта, равная отношению
интенсивности нагрузки q к объемному весу грунта
где h - приведенная высота слоя грунта, равная отношению
интенсивности нагрузки q к объемному весу грунта 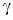 . .
При расчетах гидрометрических
сооружений часто приходится иметь дело с грунтом, находящимся во
взвешенном состоянии. Для таких условий в формулы (12-3) - (12.7)
надо подставлять объемный вес взвешенного грунта и его же угол внутреннего
трения" который в среднем можно принимать на 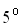 меньше, чем
меньше, чем 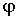 для сухого грунта. для сухого грунта.
Определив силы, действующие
на стенку, приступают к оценке ее устойчивости. Устойчивость на
сдвиг оценивается коэффициентом устойчивости на сдвиг 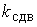 ,
который представляет собой отношение силы, удерживающей стенку,
а это сила трения ,
который представляет собой отношение силы, удерживающей стенку,
а это сила трения 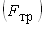 ,
к силе сдвигающей, т. е. давлению грунта. На рис. 12.2, 12.3 ,
к силе сдвигающей, т. е. давлению грунта. На рис. 12.2, 12.3 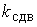 равен
равен
здесь f - коэффициент трения (ориентировочные значения его
можно брать по табл. 7.3).
Стенка считается устойчивой,
если
Устойчивость на опрокидывание
оценивается коэффициентом устойчивости на опрокидывание 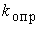 ,
который представляет собой отношение удерживающего момента ,
который представляет собой отношение удерживающего момента 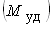 ,
создаваемого весом стенки, к опрокидывающему моменту ,
создаваемого весом стенки, к опрокидывающему моменту 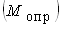 ,
возникающему от давления грунта. ,
возникающему от давления грунта.
Моменты (произведение
силы на плечо) рассчитываются относительно того ребра, вокруг которого
стенка может опрокинуться. На рис. 12.2 - это ребро A. Здесь:
Для обеспечения устойчивости требуется
Устойчивость стенки на
просадку оценивается сравнением фактических напряжений, возникающих
по основанию стенки, с расчетным сопротивлением грунтов (см. табл.
7.4), при этом первые не должны превышать вторых.
Фактические напряжения
рассчитывают по формулам сложных сопротивлений (см. п. 9.7). Если
линия действия силы G (веса стенки) проходит через центр
основания (рис. 12.2), то напряжения равны
Здесь F = b - площадь, a 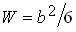 - момент сопротивления прямоугольного сечения, каким является основание
стенки (напомним: длина стенки 1 м); знаки (-) и (+) характеризуют
соответственно сжатие и растяжение;
- момент сопротивления прямоугольного сечения, каким является основание
стенки (напомним: длина стенки 1 м); знаки (-) и (+) характеризуют
соответственно сжатие и растяжение; 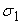 и
и 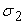 - напряжение в точке A
и в точке В. Между этими точками напряжение меняется линейно. - напряжение в точке A
и в точке В. Между этими точками напряжение меняется линейно.
Если линия действия силы
G не проходит через центр основания (рис. 12.3), т. е. имеет
место внецентренное сжатие, то для расчета напряжений поступают
следующим образом.
Сначала находят местоположение
так называемого центра давления с, представляющего собой
расстояние от точки А до того места, где равнодействующая
сил G и 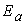 пересекает линию
основания стенки пересекает линию
основания стенки
Затем определяют эксцентриситет равнодействующей е:
Наконец вычисляют напряжение по формулам:
В заключение сравнивают найденное напряжение с расчетным сопротивлением.
Расчет якорей
подвесных гидрометрических мостиков, люлечных, паромных и лодочных
переправ выполняют с целью оценки их устойчивости под действием
усилий со стороны несущих канатов мостиков (см. рис. 4.3) или ездовых
канатов переправ (см. рис. 4.14). Расчет якорей мостиков и переправ
производится одинаково. Рассмотрим методику такого расчета на примере
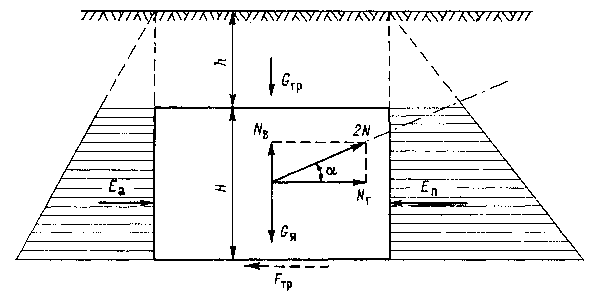
бетонного якоря, изображенного на рис. 12.5. Размеры якоря, глубина
его заложения и угол наклона тяг 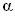 ,
к которым крепятся канаты, известны. ,
к которым крепятся канаты, известны.
| |
Рис. 12.5. Схема к расчету устойчивости якоря. |
Устойчивость якоря проверяют
на сдвиг и выдергивание. Сдвинуться он может под влиянием горизонтальной
составляющей 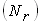 натяжения двух
канатов (2N), а выдернуть его может вертикальная составляющая натяжения двух
канатов (2N), а выдернуть его может вертикальная составляющая
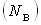 . .
Кроме усилия от канатов
к якорю приложены следующие основные силы: собственный вес якоря
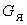 , вес
грунта над якорем , вес
грунта над якорем 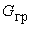 ,
сила трения по площади основания якоря ,
сила трения по площади основания якоря 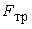 ,
активное давление грунта на заднюю грань якоря ,
активное давление грунта на заднюю грань якоря 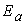 ,
пассивный отпор грунта по передней грани якоря ,
пассивный отпор грунта по передней грани якоря 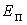 .
Рассмотрим, как находить значение этих сил. Вес якоря и грунта определяется
элементарно. Горизонтальная и вертикальная составляющие натяжения
канатов соответственно равны: .
Рассмотрим, как находить значение этих сил. Вес якоря и грунта определяется
элементарно. Горизонтальная и вертикальная составляющие натяжения
канатов соответственно равны:
Напомним, что способы определения усилия в канате (N) рассмотрены
в главе 11. Силу трения находим как:
где f - коэффициент трения (см. табл. 7.3).
Активное давление грунта
вычисляем по формуле (12.5). С учетом ширины якоря b (из
плоскости чертежа) 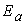 равно: равно:
Теперь обратим внимание
на расчет пассивного отпора 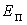 .
В отличие от активного давления грунта, которое возникает, когда
конструкция (стенка, якорь) стремится отодвинуться от грунта, пассивный
отпор имеет место в том случае, когда конструкция под влиянием какой-то
силы (например, .
В отличие от активного давления грунта, которое возникает, когда
конструкция (стенка, якорь) стремится отодвинуться от грунта, пассивный
отпор имеет место в том случае, когда конструкция под влиянием какой-то
силы (например, 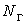 ) стремится
надвинуться на грунт. Рассчитывают ) стремится
надвинуться на грунт. Рассчитывают 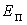 по формуле
по формуле
Формулы (12.12) и (12.13) отличаются друг от друга знаком в скобках
после 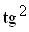 . .
Устойчивость якоря на
сдвиг оценивается так же, как подпорной стенки, т. е. по коэффициенту
устойчивости на сдвиг (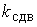 ), который
в данном случае имеет вид: ), который
в данном случае имеет вид:
Устойчивость якоря на
выдергивание оценивается коэффициентом устойчивости на выдергивание
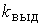 , представляющим собой, как
и рассмотренные выше коэффициенты устойчивости, отношение сил, удерживающих
тело, к силам, вызывающим возмущение: , представляющим собой, как
и рассмотренные выше коэффициенты устойчивости, отношение сил, удерживающих
тело, к силам, вызывающим возмущение:
Расчет шпунтов (см.
рис. 3.4) и одиночных свай на горизонтальную нагрузку весьма
сложен из-за трудностей определения закона распределения давления
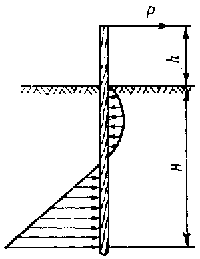
в грунте, примыкающем к шпунту (свае). Для ориентировочного расчета
максимальной горизонтальной силы 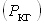 ,
не нарушающей устойчивости шпунта или сваи (рис. 12.6), предложено
несколько эмпирических формул, из которых можно рекомендовать, например,
такую: ,
не нарушающей устойчивости шпунта или сваи (рис. 12.6), предложено
несколько эмпирических формул, из которых можно рекомендовать, например,
такую:
где 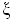 - коэффициент, имеющий значение 1 для шпунтов, 2 - для круглых свай,
и 2,6 - для квадратных свай; Н - глубина забивки; b
- ширина шпунтовой стенки или диаметр сваи; n = h/H
- отношение свободной длины шпунта к глубине его забивки;
- коэффициент, имеющий значение 1 для шпунтов, 2 - для круглых свай,
и 2,6 - для квадратных свай; Н - глубина забивки; b
- ширина шпунтовой стенки или диаметр сваи; n = h/H
- отношение свободной длины шпунта к глубине его забивки;
| |
Рис. 12.6. Схема к расчету устойчивости шпунта (сваи). |
Свая (шпунт) должна быть
не только устойчива в грунте, но и достаточно прочна, чтобы выдерживать
изгибающий момент, создаваемый силой Р. Значение, этого момента
находится по формулам:
- для 1 м погонной длины шпунтовой стенки
Прочность сваи оценивается по формуле (9.34).
|
|
|
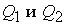 - соответственно масса
влажного и высушенного грунта;
- соответственно масса
влажного и высушенного грунта;